Set Builder Notation Vs Roster Method

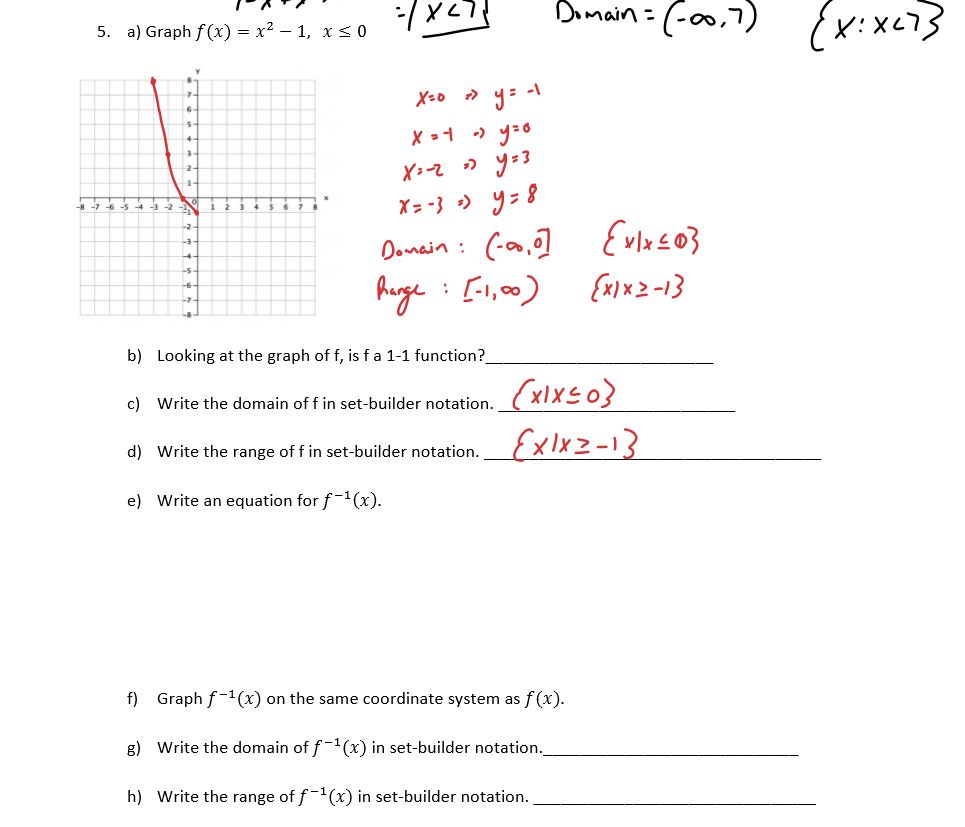
There are mainly two methods that can be used to represent a set. The Listing method is also called the roster method. This method shows the list of all the elements of a set inside brackets. The elements are written only once and are separated by commas. Rule method or set builder form in this method the elements are not listed instead, we will write the element using a variable followed by a vertical line or colon and write the general property of the same representative.

In set theory, a set X is defined as a subset of the other set Y, if all the elements of set X should be present in the set Y. This can be symbolically represented by X ⊂ Y What are the two classifications of subset? S last known address on file with the Company. Uncertificated Stock shall be deemed delivered for all purposes when the Company or a Stock transfer agent of the Company shall have given to the grantee by electronic mail or by United States mail, addressed to the grantee, at the grantee? S last known address on file with the Company, notice of issuance and recorded the issuance in its records (which may include electronic ?book entry? records).

The Administrator may place legends on any Stock certificate or notation on any book entry to reference restrictions applicable to the Stock. The roster notation is a simple mathematical representation of a set in mathematical form. In this method, the elements are enumerated in a row inside the curly brackets. If the set contains more than one element, then every two elements are separated by a comma symbol. The contents of a set can be described by listing the elements of the set, separated by commas, inside a set of curly brackets. This way of describing a set is called roster form .

In this set, the curly brackets represent a set. Inside the curly braces, a variable, a separator and a logical predicate are written one after one for expressing a set in a mathematical form. In the above form, $x$ is a variable, colon or vertical bar is a separator and $s$ is a formula that the one or more common properties of the objects . The symbol 2 is used to describe a relationship between an element of the universal set and a subset of the universal set, and the symbol \(\subseteq\) is used to describe a relationship between two subsets of the universal set.

For example, the number 5 is an integer, and so it is appropriate to write \(5 \in \mathbb\). It is not appropriate, however, to write \(5 \subseteq \mathbb\) since 5 is not a set. It is important to distinguish between 5 and .

The difference is that 5 is an integer and is a set consisting of one element. Consequently, it is appropriate to write \(\ \subseteq \mathbb\), but it is not appropriate to write \(\ \in \mathbb\). The distinction between these two symbols is important when we discuss what is called the power set of a given set.

To the extent the parties to such Sale Event do not provide for the assumption, continuation or substitution of Awards, upon the effective time of the Sale Event, the Plan and all outstanding Awards granted hereunder shall terminate. S discretion or to the extent specified in the relevant Award Certificate. The Company shall also have the option to make or provide for a payment, in cash or in kind, to the grantees holding other Awards in an amount equal to the Sale Price multiplied by the number of vested shares of Stock under such Awards.

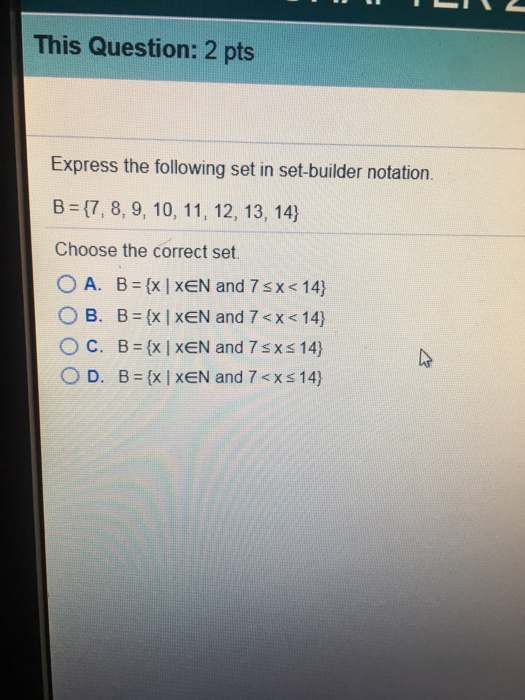
How do you write a set in roster notation? In roster notation, the elements of a set are represented in a row surrounded by curly brackets and if the set contains more than one element then every two elements are separated by commas. In set builder notation, we define a set by describing the properties of its elements instead of listing them. This method is especially useful when describing infinite sets. Set-builder notation is defined as a representation or a notation that can be used to describe a set that is defined by a logical formula that simplifies to true for an element of the set.

The set builder notation includes one or more than one variable. It also defines a rule about the elements which do not belong to the set and which elements belong to the set. Let us read about different methods of writing sets.

The whole thing is supposed to be enclosed in curly brackets but LaTeX apparently can't render them here. There's some symbols I'm guessing you haven't seen so I'll explain those. In set notation the e-shaped symbol means "is an element of" and the vertical bar means "such that". And hopefully you already know R denotes the real numbers.

So in English the above notation can be read as "the set of all real numbers x such that a is less than x and x is less than b." The roster method is defined as a way to show the elements of a set by listing the elements inside of brackets. An example of the roster method is to write the set of numbers from 1 to 10 as . An example of the roster method is to write the seasons as . Mathematics is working on the basis of rules or formulas. So, the idea had come to express a set constructively in a special mathematical notation by defining the properties of elements in a formula.

Hence, the constructive representation of a set in a mathematical rule is called the set-builder notation. Set Builder Notations is the method to describe the set while describing the properties and not just listing its elements. When there is set formation in a set builder notation then it is called comprehension, set an intention, and set abstraction. In Mathematics, set builder notation is a mathematical notation of describing a set by listing its elements or demonstrating its properties that its members must satisfy. Subject to Section 3 hereof, if, as a result of any reorganization, recapitalization, reclassification, stock dividend, stock split, reverse stock split or other similar change in the Company? The adjustment by the Administrator shall be final, binding and conclusive.

No fractional shares of Stock shall be issued under the Plan resulting from any such adjustment, but the Administrator in its discretion may make a cash payment in lieu of fractional shares. It is important to know set builder notation, especially in mathematics, because it allows you to group together large number of elements that belong to a certain category. The above set has only 3 elements, so it would not be difficult to write it in roster form as shown above. However, if your set has hundreds or thousands of elements, it would be hard to list them out, but easy to refer to them using set builder notation.

The set of integers is represented by the letter Z. Integers are sometimes split into 3 subsets, Z+, Z- and 0. Z+ is the set of all positive integers , while Z- is the set of all negative integers (, -3, -2, -1). Zero is not included in either of these sets . A set with no members is called an empty, or null, set, and is denoted ∅. Because an infinite set cannot be listed, it is usually represented by a formula that generates its elements when applied to the elements of the set of counting numbers.

In sets theory, you will learn about sets and it's properties. It was developed to describe the collection of objects. You have already learned about the classification of sets here. The set theory defines the different types of sets, symbols and operations performed. The elements in a set can be represented in a number of ways, some of which are more useful for mathematical treatment and others for general understanding.

These different methods of describing a set are called set notations. There are some special symbols that we use for common sets. The symbol is used to denote the set of natural number. These are the counting numbers or positive whole numbers. The symbol is used for the set of integers. These are the natural numbers together with zero and the negative whole numbers.

We use to indicate that an element belongs to a set. The set can be defined by listing all its elements, separated by commas and enclosed within braces. In Preview Activity \(\PageIndex\), we worked with verbal and symbolic definitions of set operations.

However, it is also helpful to have a visual representation of sets. Venn diagrams are used to represent sets by circles drawn inside a rectangle. The points inside the rectangle represent the universal set \(U\), and the elements of a set are represented by the points inside the circle that represents the set. For example, Figure \(\PageIndex\) is a Venn diagram showing two sets. The roster method lists all the elements or members in the set, whereas a description in words explains what elements are in the set using a sentence.

And set-builder notation expresses how elements are given membership in the set by specifying the properties that define the collection of objects. In Python, the set-builder's braces are replaced with square brackets, parentheses, or curly braces, giving list, generator, and set objects, respectively. Python uses an English-based syntax. Haskell replaces the set-builder's braces with square brackets and uses symbols, including the standard set-builder vertical bar.

Therefore, set builder notation is a method of writing sets often with an infinite number of elements. It is commonly used with rational numbers, real numbers, complex numbers, natural numbers, and many more. This notation can also be used to express sets with intervals and equations. But the problem arises when we have to list elements lying inside either the small intervals or a very large set of numbers, or even an infinite set. Using roster notation does not make sense and is a very tedious method.

Therefore, we use set-builder notation for such conditions. Set builder notation is defined as a mathematical notation used to describe a set using symbols. It is used to explain elements of sets, relationships, and operations among the sets. A collection of numbers, elements that are unique can be described as a set. Set-builder notation is a representation used to write sets, often for sets with an infinite number of elements.

It is used with common types of numbers, such as integers, real numbers, and natural numbers. This notation can also be used to express sets with an interval or an equation. Treasury stock, stock options, equity participation units, warrants, preferred stock, convertible stock, and rights are not part of the float.

Shares held in a trust to allow investors in countries outside the country of domicile, such as depositary shares and Canadian exchangeable shares, are normally part of the float unless those shares form a control block. If a company has multiple classes of stock outstanding, shares in an unlisted or non-traded class are treated as a control block. Subsets are a part of one of the mathematical concepts called Sets. A set is a collection of objects or elements, grouped in the curly braces, such as .

Of any set \(A\) is the set of all subsets of \(A,\) including the empty set and \(A\) itself. It is denoted by \(\mathcal\left( A \right)\) or \(.\) If the set \(A\) contains \(n\) elements, then the power set \(\mathcal\left( A \right)\) has \(\) elements. This method involves specifying a rule or condition which can be used to decide whether an object can belong to the set. This rule is written inside a pair of curly braces and can be written either as a statement or expressed symbolically or written using a combination of statements and symbols.

Some sets cannot be specified using the roster method. For instance, a set may contain infinitely many elements. In these situations, we use set builder notation.

With this notation, we specify a condition that elements must meet in order to belong to our set. For example defines the set to contain all natural numbers that are greater than 100. Before beginning this section, it would be a good idea to review sets and set notation, including the roster method and set builder notation, in Section 2.3. In this, a rule, or the formula or the statement is written within the pair of brackets so that the set is well defined.

In the set builder form, all the elements of the set, must possess a single property to become the member of that set. In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by enumerating its elements, or stating the properties that its members must satisfy. The method of defining a set by describing its properties rather than listing its elements is known as set builder notation. Set-builder notation comes in handy to write sets, especially for sets with an infinite number of elements. Numbers such as integers, real numbers, and natural numbers can be expressed using set-builder notation. A set with an interval or an equation can also be expressed using this method.

The Administrator may grant Dividend Equivalent Rights under the Plan. A Dividend Equivalent Right is an Award entitling the grantee to receive credits based on cash dividends that would have been paid on the shares of Stock specified in the Dividend Equivalent Right if such shares had been issued to the grantee. A Dividend Equivalent Right may be granted hereunder to any grantee as a component of an award of Restricted Stock Units or as a freestanding award. The terms and conditions of Dividend Equivalent Rights shall be specified in the Award Certificate. Dividend equivalents credited to the holder of a Dividend Equivalent Right may be paid currently or may be deemed to be reinvested in additional shares of Stock, which may thereafter accrue additional equivalents. Any such reinvestment shall be at Fair Market Value on the date of reinvestment or such other price as may then apply under a dividend reinvestment plan sponsored by the Company, if any.

Dividend Equivalent Rights may be settled in cash or shares of Stock or a combination thereof, in a single installment or installments. The Administrator may grant Restricted Stock Units under the Plan. A Restricted Stock Unit is an Award of stock units that may be settled in shares of Stock upon the satisfaction of such restrictions and conditions at the time of grant.

Conditions may be based on continuing employment and/or achievement of pre-established performance goals and objectives. The terms and conditions of each such Award shall be determined by the Administrator, and such terms and conditions may differ among individual Awards and grantees. Except in the case of Restricted Stock Units with a deferred settlement date that complies with Section 409A, at the end of the vesting period, the Restricted Stock Units, to the extent vested, shall be settled in the form of shares of Stock. Restricted Stock Units with deferred settlement dates are subject to Section 409A and shall contain such additional terms and conditions as the Administrator shall determine in its sole discretion in order to comply with the requirements of Section 409A. MLPF&S and BofAS may repurchase and resell the notes, with repurchases and resales being made at prices related to then-prevailing market prices or at negotiated prices, and these will include MLPF&S? S trading commissions and mark-ups or mark-downs.